Proyecto Geometría y arte
Proyecto realizado por la docente:Alba Fuks subido a Integrar.edu.ar
Fundamentación:
Proyecto realizado por la docente:Alba Fuks subido a Integrar.edu.ar
Numerosas investigaciones de diferentes países de Latinoamérica dan cuenta de que, en la escuela primaria se deja de lado la geometría y que se subestima la adquisición de los conocimientos espaciales y geométricos.
Mientras que para otros conocimientos, las prácticas de la enseñanza de la matemática se basan en la resolución de problemas, en el trabajo con geometría parecen estar ausentes, privilegiándose actividades centradas en la presentación de los objetos geométricos y sus propiedades.(Héctor Ponce, 2000).
Las dificultades para comprender la generalidad y la particularidad de las figuras y cuerpos geométricas se refuerza didácticamente por la presentación casi exclusiva de representaciones estereotipadas .Las figuras geométricas se representan siempre en las mismas posiciones, el cuadrado solo puede representarse apoyado en un lado, pues si la figura se apoya en un vértice ya pasa a llamarse rombo, este tipo de representaciones hace que el alumno piense que la posición también es una de las características de la figura y que en otras construcciones o situaciones no pueda reconocerlas fácilmente. Sin embargo, que un alumno aprenda geometría va más allá de que pueda reconocer, nombrar y representar figuras y cuerpos, sino que debe propiciarse la búsqueda de relaciones entre sus elementos, a través de la observación, comparación y construcción. Debe verbalizar y escribir las relaciones que descubre, proponer conjeturas sencillas que con los otros alumnos y el docente discutirán y validarán durante la clase de matemática.
El objetivo de este proyecto es redescubrir que es posible enseñar geometría, de modo que los estudiantes puedan comprender los conocimientos que se pretende enseñar. Y tenemos como horizonte demostrar que se puede proponer en la escuela situaciones de enseñanza en las que se realicen los juegos para enseñar geometría. Se trata de que la enseñanza esté basada en la resolución de problemas, sea dinámica más que estática, propiciando que las actividades tiendan a enriquecer los conceptos y las imágenes conceptuales de los objetos geométricos que estudian.
Con la realización de este trabajo pretendemos la consecución de nuevos y diversos conocimientos que de seguro serán bastante útiles en el resto de la vida escolar de nuestros alumnos y que le proporcionará una formación completa.
Por último deseamos valorizar y recordar la importancia de incluir el juego y el arte para aprender matemática, que despierte el interés y permita en muchos casos enseñar sobre el área de una manera más integral.
Objetivos generales:
- Vincular la Matemática con el arte.
- Conocer y comprender los recursos gráficos que aporta la geometría al arte.
- Descubrir formas geométricas en el entorno inmediato: naturaleza, construcciones arquitectónicas, objetos cotidianos.
- Aplicar las propiedades de las figuras en el arte y en el diseño.
- Conocer las obras de pintores como: Kandisky, Paul Klee, Kazimir Malevich's,
- Valorar las ventajas del trabajo cooperativo en grupo para adquirir y producir conocimientos y como vía para desarrollar la capacidad de comunicarse, crear y razonar.
Actividades:
1) Comenzamos a trabajar con el vitraux
1) ¿Cuáles son los elementos de un triángulo?
2) Problema:
Sergio dice que el ángulo llano mide dos rectos, pero Daniela asegura que mide 180°. ¿Quién tiene razón?
Te animas a marcar un ángulo llano
4) Hay algún triángulo que tenga ángulo obtuso.
Investiga: ¿Qué es un vitraux?
2) Comenzamos a conocer a algunos pintores: Vasarely Kandinsky
El 16 de diciembre de 1866 (4 de diciembre del antiguo calendario ruso) nacía en Moscú Vasili Kandinski (o traducido Vasili Vasílievich), precursor de la abstracción en pintura y teórico del arte. Se considera que con él comienza la abstracción lírica tendencia que se desarrolló a partir de 1910 con la Primera acuarela abstracta. Si bien estudió derecho y economía, más tarde se dedicó por completo al arte.
Cuando Kandinsky miraba el cuadro no era para él lo mas importante los objetos que aparecían en el mismo sino los colores de formaban parte del mismo y la fuerza que estos adquirían en la obra.
¿Qué herramientas utilizó este pintor para realizar sus cuadros?
¿En cuáles hace falta elementos de la geometría?¿Cuáles?
¿Qué conceptos tuvo que tener en cuenta?
¿Por qué suponen que para este artista es importante la geometría en sus cuadros?
Trabajaremos ahora en profundidad sobre este cuadro:
¿Qué figuras o rectas puedes observar?
¿Cuántas rectas hay?
¿Y en esta composición cuántas figuras hay superpuestas, se animan a contarlas?
¿Todas las rectas son iguales?
Rectas
¿Qué tipo de rectas utilizó el pintor para poder lograr el cuadro?
¿Cuales reconoces?
¿Cuales reconoces?
¿Cuántas utilizó en total para lograr por ejemplo “el barco”?
¿Te parece creativo? ¿Por qué?
¿Todas las conservan el mismo grosor? ¿Qué logra con esto?
ELEMENTOS QUE CONSIDERÓ DE LA GEOMETRÍA
¿Cuántas polígonos ves?¿Cuáles reconoces?
Realizamos cuadros con mapas conceptuales en carpeta a medida que avance el proyecto.
ALGUNOS CONCEPTOS MÁS DETALLADOS...
Polígonos: El polígono es una figura geométrica plana limitada por unos segmentos que se denominan lados.
ENLACE PARA JUGAR CON POLÍGONOS
ELEMENTOS DE GEOMETRÍA
SEGMENTOS¿Cómo trazar segmentos congruentes con regla y compás?
DOS SEGMENTOS SON CONGRUENTES CUANDO TIENEN LA MISMA LONGITUD., ES DECIR, EL MISMO LARGO.
Clases de líneas:
Como ya sabes, existen varias clases de líneas. La línea RECTA y la línea CURVA. Además están otras líneas que podemos formar
Línea quebrada
línea Mixta
Línea Ondulada
Línea Espiral
RECTAS
Les dejo dos enlaces para que puedas aprender jugando… no te olvides de hacerlos hasta el final… porque te servirán para repasar todo lo que hemos trabajado en clase.
Acuérdate de que las líneas también pueden ser:
Dos rectas son SECANTES…. cuando tienen un punto en común, es decir, si se cortan.
Dos rectas son PARALELAS si no tienen ningún punto en común, es decir, si no se cortan nunca.
ENLACE PARA PRACTICAR
ENLACE PARA PRACTICAR RECTAS Genmatic.org
ENLACE PARA DIBUJAR RECTAS Y CORRECCIÓN AUTOMÁTICA Librosvivos.net
Videos para repasar lo visto en clase.
RECTAS PARALELAS
Podés hacerlo con dos escuadras o con una regla y escuadra.
RECTAS PERPENDICULARES
RECUERDA QUE PUEDES DIBUJARLO CON UNA REGLA Y UNA ESCUADRA TAMBIÉN, COMO TE MOSTRÉ.
OTRA FORMA DE TRAZAR PARALELAS Y PERPENDICULARES
VIDEO DE 1 MINUTO
Ángulos:
http://contenidosdigitales.ulp.edu.ar/exe/articulacion_mat/rectas_y_ngulos.html
Escucha la introducción avanzando con la tecla inferior derecha y te darás cuenta de la importancia que tienen los ángulos en nuestras rutinas diarias.
Según la medida de esta amplitud se clasifican los diferentes ángulos.
Así los encontramos rectos, aquellos que miden exactamente 90º, llanos, aquellos que miden exactamente 180º y, a partir de estos dos, clasificamos los demás:
Agudos: si miden menos de 90º hasta 1°
Obtusos: si miden más de 90º hasta 179°
Cóncavos: si miden menos de 180º
Convexos: si miden más de 180º
Nulo, si miden 0°
Ángulo: porción de plano delimitada por dos semirrectas con origen común.
Según la medida de esta amplitud se clasifican los diferentes ángulos.
Así los encontramos rectos, aquellos que miden exactamente 90º, llanos, aquellos que miden exactamente 180º y, a partir de estos dos, clasificamos los demás:
Agudos: si miden menos de 90º hasta 1°
Obtusos: si miden más de 90º hasta 179°
Cóncavos: si miden menos de 180º
Convexos: si miden más de 180º
Nulo, si miden 0°
Ahora que hemos entendido qué son los ángulos y sabemos identificarlos necesitamos a definir sus elementos, ya que son aquello que nos va a permitir analizarlos y reproducirlos. Cómo has visto en la imagen, se componen de los siguientes elementos elementos:
a: uno de los dos lados, es decir, una de las dos semirrectas que compone el ángulo. Junto con el otro lado delimita la amplitud del ángulo.
b: lado dos; con el mismo origen que el otro lado (a), completa el ángulo y delimita su amplitud.
C: vértice. Es el origen común de ambas semirrectas.
α: amplitud del ángulo cóncavo que forman las dos semirrectas.
β: amplitud del ángulo convexo que forman las dos semirrectas.
Actividad N° 1 Rectas y ángulos
Actividad N°2 Recorrido con giros
Actividad N°3 Medimos con transportador
Rectas y ángulos Teoría y práctica Fuente: genmagic.org (OJO!! no veeremos operaciones con ángulos, ni ángulos complementarios)
Círculo y circunferencia "František Kupka"
Frantisˇek Kupka, uno de los pioneros de la abstracción, nació en una pequeña localidad de la Bohemia oriental y se formó artísticamente en Praga y Viena. Se instaló en París en 1896, donde durante un tiempo se ganó la vida como ilustrador. En la capital francesa encontró un ambiente más adecuado para el desarrollo de su pintura y recibió las influencias del neoimpresionismo, el simbolismo y el modernismo.
¿Qué conceptos de la geometría maneja este artista?
Observa esta infografía y trata de seleccionar cuáles son esos conceptos.
Para tener en cuenta
1.- LA CIRCUNFERENCIA
Es una línea curva, cerrada y plana en la que todos sus puntos están a la misma distancia de un punto interior llamado centro.
2.- ELEMENTOS DE LA CIRCUNFERENCIA:
*Centro: Punto central. Está a la misma distancia del resto de puntos de la circunferencia.
*Radio: Segmento que une el centro con un punto cualquiera de la circunferencia.
*Diámetro: Segmento que une dos puntos de la circunferencia pasando por el centro. Mide el doble que el radio.
*Semicircunferencia: Es la mitad de una circunferencia.
Ahora se agregan dos más que no conocías...
*Cuerda: Une dos puntos de la circunferencia sin pasar por el centro.
*Arco: Porción de circunferencia limitada por una cuerda.
EL CÍRCULO Es la parte de plano comprendida
dentro de la circunferencia.
- ELEMENTOS DE UN CÍRCULO: Son los mismos que la circunferencia (excepto la semicircunferencia) y tres más: Semicírculo: Mitad de un círculo.
El diámetro divide al círculo en dos semicírculos. Sector circular: Porción de círculo limitada por dos radios
y su arco. Segmento circular:
Porción de círculo limitada por una cuerda
y su arco.
Corona circular:
Corona circular es la región de plano comprendida entre dos circunferencias concéntricas (con el mismo centro).
MÁS VIDEOS CORTITOS PARA REPASAR...
¿Cómo medir ángulos?
¿Cómo apoyo el transportador? RECUERDA ES PURA PRÁCTICA.Duración: 2 minutos.
Duración 6 minutos...¡MUY POQUITO A REPASAR SE HA DICHO!
Repaso de SEGMENTOS, RECTAS, ÁNGULOS.
Estimación de ángulos. (fuente: Educaplus)
TRIÁNGULOS
Cuadros donde utilizó como figura importante el triángulo.
Spitze In Bogen, C.1927
Weiches Hart diciembre 1866
OBSERVANDO LOS CUADROS RESPONDE...
¿CUÁL DE LOS CUADROS TIENE MAYOR CANTIDAD DE TRIÁNGULOS?
¿QUÉ TIPO DE TRIÁNGULOS UTILIZÓ EN EL SEGUNDO Y TERCER CUADRO?
¿CUÁL ES LA OBRA QUE MÁS VARIEDAD DE TRIÁNGULOS UTILIZÓ?
REPASAMOS LA CLASIFICACIÓN DE TRIÁNGULOS:
ESTE VIDEO RESUME LO QUE DESCUBRIMOS ENTRE TODOS....
CLASIFICACION DE TRIANGULOS CON GEOGEBRA
ENLACE https://www.geogebra.org/m/AfUdgx2K
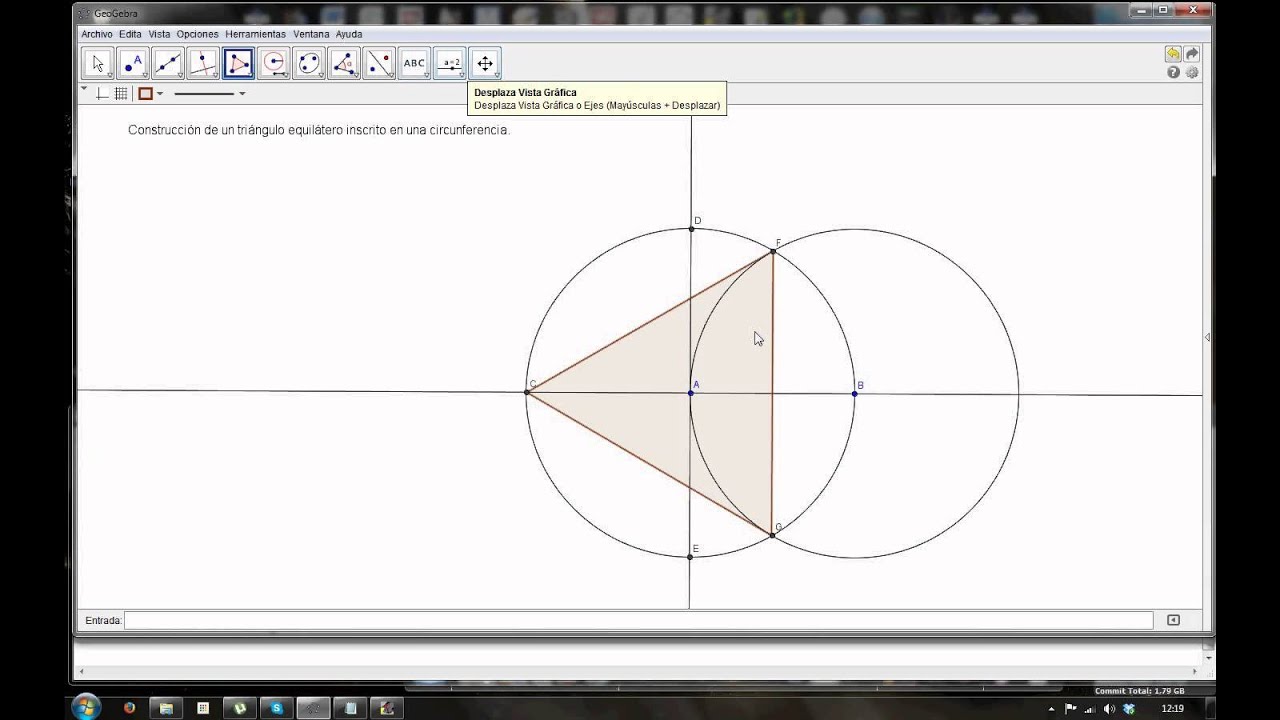
Utilización del GEOGEBRA
Triángulo equilátero con dos circunferencias
Para su construcción es necesario crear dos puntos, y tomar esos punto como centros de la dos circunferencias, damos el un tercer punto que es donde se intersecan y se trazan los segmentos.
Deberá quedarnos.
CUADRILÁTEROS
¿Qué cuadriláteros reconoces que utilizó el artista?
Aquí Mondrian
OTROS PINTORES QUE UTILIZAN CUADRILÁTEROS
Victor Vasarely
Pintor húngaro afincado en París, asociado al arte cinético. Se empeñó en incorporar la dimensión temporal a la forma plástica, camino iniciado ya por los futuristas y Duchamp. Su pintura se basa en el rigor científico y combina las leyes de la física y el conocimiento de la geometría, junto a las cualidades perceptivas del color y su influencia en la percepción visual. Su obra no se basó tanto en la belleza de las formas como en la sorpresa visual que producen, motivada por el engaño perceptivo.
Observa este otro cuadro de Vasarely
¿Cómo logra dar profundidad a su obra?
¿Qué ocurre con los cuadriláteros que eligió?
¿Cambian los ángulos o los lados?
¿Siguen siendo paralelogramos?
Composición 1970 víctor Vasarely
¿En este cuadro observas algo extraño?
¿Qué efecto causa en el espectador?
En el cuadro notamos una transformación de las figuras.
¿Qué relación existe entre un cuadrado, un rectángulo y un paralelogramo?
¿Respeta siempre el uso del cuadrilátero?
Este artista tiene muy claro ciertos relaciones entre cuadrados, paralelogramos propiamente dichos y los rombos.
¿Qué relación guarda el rombo con el cuadrado?
¿Todo rombo es un cuadrado o todo cuadrado es un rombo?
Otros pintores
Kazimir Malevich's,
Paul Klee
Resumimos conceptos
Cuadriláteros
Un cuadrilátero es un polígono que tiene cuatro lados. Los cuadriláteros pueden tener distintas formas pero todos ellos tienen cuatro vértices y dos diagonales. Otros nombres usados para referirse a este polígono son tetrágono y cuadrángulo.
Elementos de un cuadrilátero
Los elementos de un cuadrilátero son:
4 vértices: los puntos de intersección de las rectas que conforman el cuadrilátero;
4 lados: los segmentos limitados por dos vértices contiguos;
2 diagonales: los segmentos cuyos extremos son dos vértices no contiguos;
4 ángulos interiores: conformados por dos lados y un vértice común;
8 ángulos exteriores: conformados por un lado, un vértice y la prolongación del lado adyacente.
En todos los cuadriláteros la suma de los cuatro ángulos interiores es igual a 360º (grados) o 2π radianes, y la suma de los ángulos exteriores es igual a 360º o 4 rectos.
La forma más habitual de clasificar cuadriláteros es por el paralelismo de sus lados. Según este criterio los cuadriláteros pueden ser:
Sin lados paralelos. (TRAPEZOIDES).
Con al menos un par de lados paralelos. (TRAPECIOS).
Con dos pares de lados paralelos. (PARALELOGRAMOS).
Un trapezoide especial es el Romboide: tiene dos pares de lados consecutivos iguales
Los trapecios se clasifican en:
Trapecio escaleno: es el que tiene todos sus lados de distinta longitud (desiguales).
Trapecio rectángulo: es el que tiene dos ángulos rectos.
Trapecio isósceles: tiene los ángulos adyacentes a las bases iguales y los dos lados no paralelos también son iguales.
PARALELOGRAMOS ESPECIALES:
Rectángulo: tiene sus 4 ángulos rectos (90º)
Rombo: tiene sus 4 lados iguales.
Cuadrado: tiene sus 4 lados iguales y sus 4 ángulos rectos
TENIENDO EN CUENTA SUS DIAGONALES
Propiedades de las diagonales
Un cuadrilátero tiene dos diagonales.
1-Por su longitud pueden ser: a) Congruentes. b) No congruentes.
2-Por su disposición:
a) Se cortan
Y por su posición pueden ser: i)Oblicuas. ii)Perpendiculares
Y por su punto de intersección: i)Se cortan en el punto medio. ii)Una corta a la otra en su punto medio. iii)Se cortan en otro punto cualquiera.
b) No se cortan
Propiedades de las diagonales
En todo cuadrángulo convexo las diagonales se cortan en un punto interior al mismo.
Si las diagonales de un cuadrilatero se cortan en un punto medio, dicho cuadrilátero es un paralelogramo.
Si las diagonales de un paralelogramo son perpendiculares, el paralelogramo es un rombo.
Si un cuadrilátero tiene diagonales perpendiculares y una corta a la otra en partes congruentes, dicho cuadrilátero es un romboide.
La diagonal principal del romboide es bisectriz del par de ángulos opuestos correspondientes.
Si las diagonales de un cuadrilátero son congruentes y se cortan en el punto medio, dicho cuadrilátero es un rectángulo.
Si las diagonales de un rectángulo son perpendiculares, dicho rectángulo es un cuadrado.
Recordando que:
Un paralelogramo es un cuadrilátero que tiene los lados opuestos iguales. Los ángulos opuestos son iguales y los consecutivos suplementarios. Las diagonales se cortan en el punto medio.
Visita los siguientes enlaces:
Esquema que resume todo...
COMENZAMOS CON EL TRABAJO CON EL TANGRAM
EL TANGRAM
Historia del TANGRAM
El tangram es un rompecabezas de origen chino que probablemente apareció hace tan sólo 200 ó 300 años. Los chinos lo llamaron "tabla de sabiduría" y "tabla de sagacidad" haciendo referencia a las cualidades que el juego requiere.
La misma palabra "tangram" es un invento occidental: Se supone que fue creada por un norteamericano aficionado a los rompecabezas, quien habría combinado tang, una palabra cantonesa que significa "chino", con el sufijo inglés gram (-grama) que significa "escrito" o "gráfico" (como en cardiograma).
Los primeros libros sobre el tangram aparecieron en Europa a principios del siglo XIX y presentaban tanto figuras como soluciones. Se trataba de unos cuantos cientos de imágenes en su mayor parte figurativas como animales, casas y flores... junto a una escasa representación de formas abstractas.
A lo largo del siglo XIX aparecieron diversos libros de tangram chinos, que fueron copiados por las editoriales europeas, buena prueba de la popularidad que había adquirido el juego. A partir de 1818 se publicaron libros de tangram en EE. UU., Inglaterra, Francia, Alemania, Austria e Italia.
POLÍGONOS A PARTIR DEL TANGRAM
Tangram chino: “Juego de los siete elementos” o “tabla de la
sabiduría”.
Es un juego planimétrico porque todas las figuras deben estar contenidas en un
mismo plano
1 cuadrado
5 triángulos (rectángulos isósceles):
– 2 triángulos “grandes” (los catetos miden el doble de la medida del lado del
cuadrado).
– 1 triángulo “mediano” (la hipotenusa mide el doble de la medida del lado del
cuadrado).
– 2 triángulos “pequeños”(los catetos son congruentes a los lados del
cuadrado).
1 paralelogramo
Entrar http://www.docente.mendoza.edu.ar/matematica/tangram.htm a
jugar y formar varias de las figuras que allí proponen.
9. Realización de Trabajo práctico
Consultar la pàgina http://www.slideshare.net/octavio5b/los-poligonos
y
responder en el cuaderno de actividades:
Cuadros en la Matemática https://es.slideshare.net/lilithhd3/cuadrilateros-24993912
Continuaremos....






















































